1 Risk
1.1 The Game
- Domain: the dice battles, not the board game
- Attacker and Defender each have some number of units
- Units battle with die rolls in successive rounds
- Attacker goal: destroy all Defender units
- Defender goal: reduce Attacker units to 1
1.2 Battle Unit Rules
- Attacker has A units, Defender has D units
- Attacker can use min(3, A-1)
- Defender can use min(2, D)
1.3 Battle Dice Rules
- A and D rolls are sorted in descending order and zipped
- e.g. A {4,1,3} and D {4,2} -> [(4,4), (3,2)]
- Defender has advantage: win on condition (>=)
- e.g. (4,4) -> Defender wins if 4 >= 4
1.4 Question
- Given starting number of units (A, D)…
- What is the exact probability that Attacker wins?
2 Computing Probabilities
2.1 Approach
- Find out probability of each possible battle outcome
- Chain probability of outcomes
- From game specs, there are limited battles
- [(3,2), (3,1), (2,2), (2,1), (1,2), (1,1)]
2.2 Outcome Example
- (1,1): Attacker 1 die vs Defender 1 die
- What are outcomes and associated probabilities?
- Both die can roll 1 to 6, so 36 battle permutations
- Attacker loses in 21 / 36; Defender loses in 15 / 36
2.3 Haskell Implementation
successExact :: Battlefield -> Probability
successExact (Battlefield _ 0) = 1
successExact (Battlefield 1 _) = 0
successExact b =
case M.lookup (maxTroops b) pMap of
Nothing -> 0
Just ps -> agg $ map update $ filter (not . aLoses b) ps
where update (p, losses) = (p, updateField b losses)
agg :: [(Probability, Battlefield)] -> Probability
agg pairs = foldr f 0 pairs
where f (p, b) accP = accP + (p * successExact b)
3 Results
3.1 10 x 10 Matrix
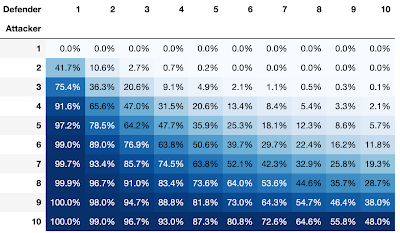
3.2 Notes
- The Rational type in Haskell gives exact results
A: 3 B: 3 | Exact: 20.61% | Exact: 692225 % 3359232
A: 3 B: 4 | Exact: 9.13% | Exact: 5520775 % 60466176
3.3 Also Interesting
- Wolfram Alpha

https://blog.wolfram.com/2017/11/20/how-to-win-at-risk-exact-probabilities/
3.4 Next Steps
- Elm visualization of probability chain!